Cachi-Forth For Modeling The Mind
Cachi Forth is a simple toy language and IDE used for modeling various AIT dynamics with a special focus on the CACHI theory of consciousness.
Cachi Forth is an open-source language and interpreter I created for the sole purpose of exploring Algorithmic Information Theory and CACHI concepts. It’s (very) loosely based on the FORTH language, which is a stack-based postfix style language.
A Cachi Forth program is a stream of instructions, which are processed from left to right. Each instruction either pushes something on the stack (which can only be a number between 0 and 127) or a command that operates on the stack in some way - like popping a value off the stack and then outputting it. There are a very limited number of instructions, but it does focus on creating abstractions that can be re-used: functions, loops, if-conditionals, prunes and branches.
Here’s a simple example:
10 out
This program has two instructions. The first pushes 10 onto the stack, and the second command pops the value off the stack and outputs it to the screen. So this program would simply output “10”.
To add two numbers, you would write it like this:
15 10 + out
This pushes 15 on the stack, then 10, then runs “+” which pops both values off the stack, adds them together, and pushes the result on the stack (replacing them). Then it runs “out” which outputs the top item on the stack, which is the result: 25.
A full specification of the language is included at the end of this article.
Why FORTH?
Forth may seem like an archaic language - it was designed to be simple enough to fit on the earliest 8 bit computers with hardly any memory. Yet the simplicity has one very large advantage: forth is very “mutation” friendly. It’s also very easy to create a random program that actually does something.
It’s mutation friendly because you can replace any instruction in the program and it will still function - there’s no structured syntax to worry about, which would make it much harder to mutate. A forth program can never produce an error, and the strict limit on execution steps means it can never get caught in a loop. This makes it very robust for running thousands of tests unattended, and a perfect setup for Monte-Carlo simulations - essential given the complexity involved.
And this is exactly why the forth interpreter was created: to run Monte-Carlo simulations to understand the dynamics of specific abstraction models, specifically under CHI constraints, which otherwise would be far too complex to calculate.
Modeling the Physiology of the Brain
The language itself is uniquely suited for modeling neural dynamics because it captures the essence of decentralized, stack-based computation and recursive abstraction expansion, both of which are hallmarks of neural processing. Unlike traditional programming languages that rely on global or scoped variables and linear control flow, Cachi-Forth operates purely on a value stack with immutable, local state - mirroring how neurons process signals via local interactions and propagate activity without centralized control. Its minimalistic instruction set, coupled with support for branching, conditional execution, and user-defined functions, enables the emergence of highly non-linear, dynamic patterns from simple rules - just as complex behavior in the brain emerges from the interaction of simple spiking neurons.
Furthermore, Cachi-Forth's architecture enforces execution through a bounded timeslice model, which reflects the temporal constraints of real neural computation. The ability to define recursive functions with arity-based arguments (rather than named variables) mimics the modular yet flexible reuse of patterns in cortical circuits. More critically, its branching and conditional blocks simulate how neuronal assemblies split into competing or cooperating subnetworks depending on input conditions. Because execution is strictly stack-based, all information flow is explicitly local and compositional, encouraging a style of program evolution that naturally reflects the emergent semantics and temporal scaffolding found in biological systems. This makes Cachi-Forth not only a toy model for computation, but a powerful language for simulating the algorithmic skeleton of inference and learning in neural substrates.
Cachi-Forth also mirrors key aspects of neural physiology by modeling execution as a sequence of localized, energy-limited operations. Just as neurons fire in discrete spikes under metabolic constraints, Cachi-Forth programs are bounded by a timeslice execution limit, simulating the resource limitations of biological systems. The stack acts analogously to a neuron's membrane potential and local state - transient, context-sensitive, and sensitive to ordering - while the program’s instructions reflect the discrete, spike-like transformations applied to inputs. The branching instructions resemble divergent axonal projections, where a single output can fork into parallel pathways, each pursuing different interpretations or reactions. Even the lack of named variables parallels the stateless, address-free interactions in neural tissue, where signal identity is carried not by symbolic reference but by routing and temporal dynamics. This alignment allows Cachi-Forth to serve as both a computational and physiological metaphor for the mind’s machinery.
Language Features
While the language is very simple, it does have some unique features.
Loops: The loop command will repeat everything after loop up to the corresponding “end” command for the number of times defined on the stack when the loop was encountered. You can nest loops.
Branch: The branch command (branch2, branch3, branch4 or branch5) will take the next N instructions (or blocks, if they are block commands) and spawn each in a separate parallel thread. Each thread will continue the rest of the code after those instructions in parallel. For example: “branch2 10 15 out” will start two threads - one putting 10 on the stack, the other putting 15 on the stack, both continuing with the program to run “out”. The output in this case would be 10 and 15. Branches can also be nested, allowing for quite complex processing.
Prune: The prune command will terminate the current thread if the value on the stack is less than 65, otherwise it continues.
Functions: You can define functions that can be re-used (they start with >, and end with the “end” command), which can represent abstractions. Functions can invoke other functions or utilize control blocks like loops and branches.
If-Then Conditionals: It has a simple ifg (if-greater-than) and ifl (if-less-than) for stack-based conditional evaluation.
Bits: As well as adding a number to the stack, it can also add a partial value - called a bit - which accumulate every time the instruction is run. This can simulate cases where there is a correlation between program length and strength of value.
IDE Features
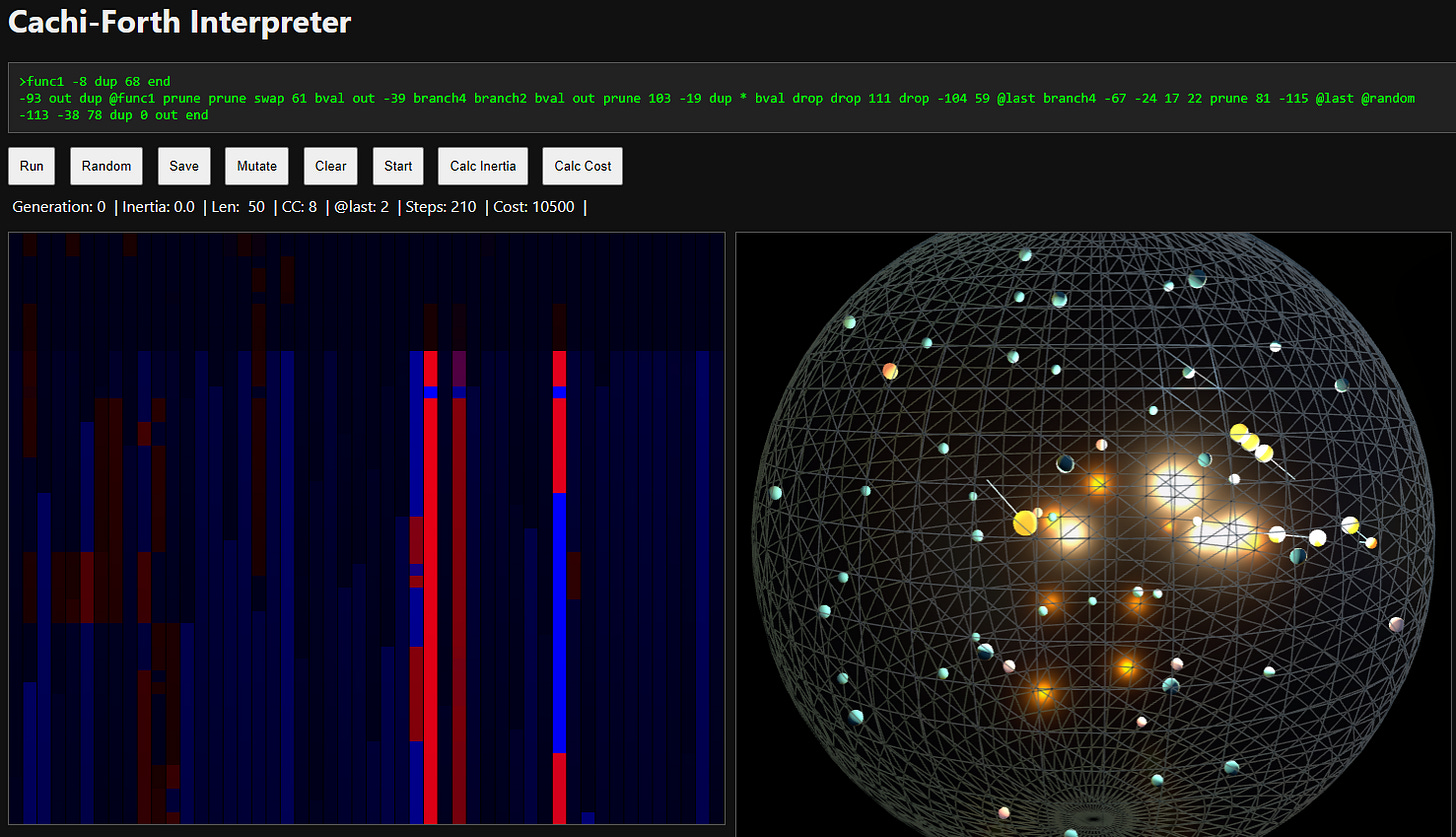
The IDE is intended to be simple, but provides an easy way to write a program and run it - with the program execution displayed visually as a sphere with points within it representing the instructions, and a snake shooting around simulating those instructions being invoked. We also show a heat map of the program, which scrolls if you start mutating the program. This shows both the cost-value of each instruction (red for high-impact, blue for low-impact), and the resilience to mutation (translucent means it was mutated recently, opaque means it is older and thus resisted mutation).
The program area at the top is where you can enter in your forth programs. Then click “Run” to run them, which will display the output underneath the buttons, and add a line with a visualization below that. The previous runs are stored as a history that scroll down, so you can see the relationship between outputs as the program evolves.
If you don’t want to create your own program, click “Random”. This will replace the current program with a 50-instruction randomly generated one. Press it a few times to get the sized output you’re looking for. Generally a program with 300-1000 steps will be a good candidate for mutations.
CACHI Modeling
Now, what’s important here is how this can model CACHI requirements for consciousness. Firstly, it will tell you the program length (Len, which is our modified Kolmogorov complexity), along with the steps it takes to execute it (Steps, which is our Computational Depth complexity). The total cost (the product of those) is displayed as Cost.
As per the CACHI formulation, if you click “Mutate” it will modify the program to maintain both the complexity cost and the identity of the program (minimizing how much changes at a time). When it modifies it, it replaces one or a few instructions with randomly generated instructions, and then runs it.
As it does this, it will display a value called “Inertia”. This is the resistance to change that the current program is exhibiting: the harder it is to change while maintaining that complexity cost, the higher the inertia.
You can click “Start” for it to continually mutate the program, while maintaining complexity cost to the best of its ability. You’ll see the program change a few times a second, along with the heatmap scrolling down the screen. Click “Stop” to stop the mutations.
You can also protect certain parts of the program. Any instructions surrounded by square brackets will not be mutated. For example:
[ 10 out ] 20 loop 1 + 10 dup out end
In this program, when you click “mutate” only the instructions from 20 and onwards will be modified - the 2 instructions in the brackets will be left alone.
Analytics
The simplicity of Cachi-Forth make it straightforward to analyze. For example, you can count the instructions in the forth program to get an approximation of Kolmogorov complexity.
There are a few other metrics we display under the program worth mentioning:
Generation: Every mutation will increment this number, so you can see how often it has mutated. Clicking Random or Clear will reset this.
Inertia: The average number of attempts that had to be made to mutate the program successfully (maintaining complexity constraints). If it’s not able to mutate it with one token after 200 turns, it’ll try mutating two tokens, and so forth.
Len: The length of (number of instructions in) the program. An approximation of the Kolmogorov complexity.
CC: The Cyclomatic Complexity, which is the number of branch points in the program.
@last: The number of @last instructions (referencing historic outputs).
Steps: The number of execution steps when running this program (the Computational Depth or Logical Depth complexity).
Cost: The Complexity Cost, which is the length multiplied by the steps.
Partition Analytics
You can also select a portion of the program to partition it and analyze how it relates to the rest of the program. There are two options you can click after selecting some of the program (for example, the body of a function):
Calc Inertia: This will calculate the inertia of just the selected instruction or program, seeing the relative cost of replacing that section with another random program. It runs through a Monte Carlo simulation to calculate this. This can be useful to indicate how fungible that part of the program is, relative to the entire program, ie. how easily replaceable the selection is. The closer to zero, the more easily replaced that selection will be. The higher (either positive or negative), the more entangled that selection is with the rest of the program, thus the harder it is to replace.
Calc Cost: This will calculate the percentage that the selected program portion contributes to the overall complexity cost. This can also give you an idea of how critical the portion is relative to the rest of the program.
Conclusion
You can read the full specs of the language here.
There’s also a Save button that will copy into the clipboard a link that will save the current program. Click that and it will open the interpreter pre-loaded so you can continue working on it.
Happy exploring!