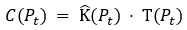Complexity as Kolmogorov and Computational Depth
A justification for calculating complexity from the *product* of Kolmogorov and Computational Depth.
CACHI posits that complexity is a two dimensional measure: when considering the complexity of an object X, we firstly, following the lead of Kolmogorov, determine the length of a program that can generate a sufficient semantically-complete copy of X (note: not necessarily the shortest program, which is incomputable). Secondly, following the lead of Charles Bennet, we determine how long that program will take to run - how many instructional-execution steps it takes to complete. This is typically known as the Logical Depth (or Computational Depth).
Why are both of these needed? Partly because the program size doesn’t tell us everything we need: firstly, what are the instructions in that program and what do they do? If there was an instruction that happened to be called “Factorize X” which did all the work of factorizing, then you could have a program of just 2 instructions that could do incredibly complex work that takes hours. Also, that program could be invoking external APIs to achieve its work. It is also utilizing hardware, including CPU and GPU processing (these days GPUs do a lot of work for you!).
So, program size alone isn’t sufficient. This is why Bennet decided that a better option was to look at the time it took to execute the program. That way even if it’s doing a lot of work in external libraries, it will still take more time to run if it takes more work to accomplish.
This is a valid point. To calculate this accurately, it wouldn’t simply be a matter of time (after all, interrupts and other aspects of computation can make that inaccurate), you would instead need to determine the number of execution steps - instructions executed in total - while also taking into account parallel invocations through multi-threading. On CPUs you can have multiple threads running in parallel on different cores, so you would need to add those together - sequentially - to get a realistic number of total steps. This becomes significantly more complex in quantum computation, but ultimately it is still tractable.
In the case of CACHI, however, neither are good enough alone. Program length isn’t sufficient, as we discussed. But steps to execute also isn’t sufficient. Only when they are put together do they tell us something important not simply about the complexity, but how the object it represents fits in to what is already provided. How it integrates. The program length actually tells you about whether it is re-using existing functionality (whether it’s pre-existing libraries, functions or hardware optimizations). The shorter it is, the more likely it is re-using existing functionality. Execution time, though, will still tell you about the overall computational complexity.
That computational complexity carries additional cost for every instruction that isn’t just invoking an existing function, because then it becomes a burden on compressibility, specifically a burden on the richness and coherence of the overall system - and in the case of CACHI, the total generated landscape.
Because of that multiplicative effect of each instruction on complexity, both aspects must be multiplied to calculate the total complexity, and in particular the complexity cost. This is why we use the formula:
The complexity of the generative program at time t is equal to the program length (K) multiplied by the total execution steps when running the program.
In CACHI, this is the value that must be kept constant, as the program evolves.
Furthermore, there's a critical cognitive analogue here: the human brain itself embodies this multiplicative relationship. The number of neurons and synaptic connections effectively bounds the "program length" of the brain, while the brain's energy budget constrains its "computational depth." Both factors are remarkably consistent throughout adulthood. This biological reality underscores the informational basis for consciousness that CACHI posits: maintaining a stable product of these complexity dimensions isn't merely a computational ideal but a physiological imperative.
Ultimately, the product formulation clarifies why deviations in complexity are costly and must be minimized or integrated within existing structures. Each non-integrated complexity increase disproportionately amplifies the cognitive load, undermining coherence and potentially destabilizing the entire system. This inherent penalty explains why consciousness favors predictable, integrable novelty rather than arbitrary, disruptive changes - emphasizing stability in the generative landscape of experience.
Outside of this, there are other justifications worth mentioning also. By having two dimensions, program length on the X axis and computational depth on the Y, we create a surface area that effectively represents the current generative program. Any increase in computational depth that has an equivalent increase in program length is necessarily non-integrated with that generative program.
This geometric representation allows us to visualize complexity in terms of areas within a bounded plane. Each point on this plane represents a unique combination of descriptive brevity (X-axis) and computational effort (Y-axis). Movement along one axis without a corresponding offset along the other indicates a shift toward non-integrated complexity - essentially, added complexity cost without leveraging existing informational structures.
Crucially, this visualization highlights why CACHI emphasizes maintaining a consistent area: expansions in surface area represent disruptions to informational coherence. If complexity expands disproportionately in one dimension without integration in the other, the generative model becomes less stable and more computationally expensive, leading to potential cognitive overload or instability.
Therefore, maintaining a stable product of these two dimensions forms a clearly delineated boundary - like a contour line of integration - defining the ideal operational zone for consciousness to emerge and persist. Any deviation that strays outside this contour line signifies an increase in complexity cost, underscoring the dynamic yet balanced nature of consciousness as a homeostatic mechanism.
This algorithmic information theoretic basis is compelling on its own, but it becomes especially relevant when considering how this quadratic cost of non-integrated computational depth mirrors the probability cost of quantum deviations, as described in the Born rule of quantum mechanics. Can this two dimensional complexity cost solve some of the most enigmatic mysteries of quantum physics? We’ll leave that for another post.