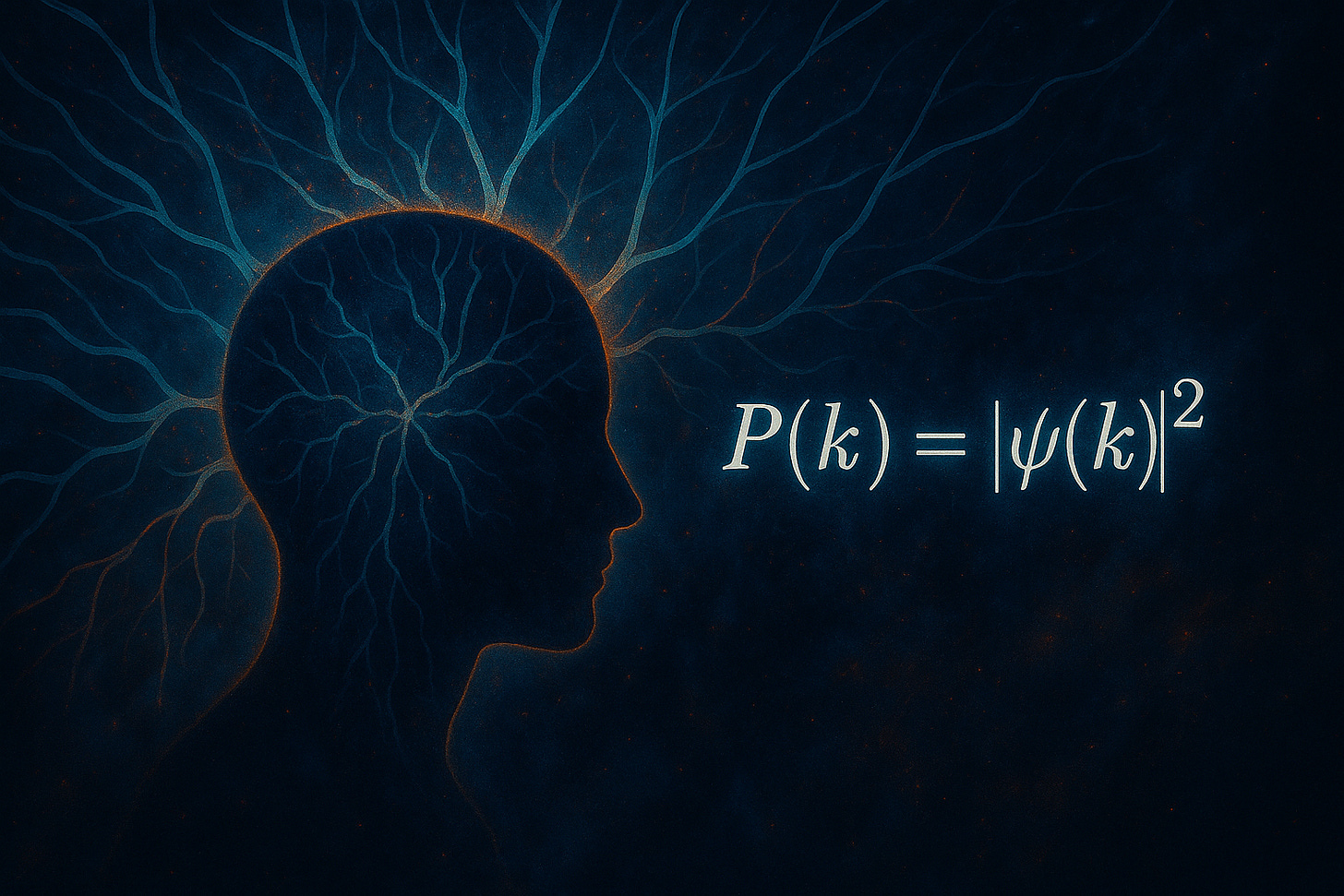Foundations of a Born Rule Derivation Part 1

Here we look at the problem of probability in quantum physics and discuss how CHI dynamics lay a foundation for a plausible solution, which we demonstrate using Cachi-Forth.

The Many Worlds Interpretation, also called Everettian Quantum Mechanics, is what Sean Carroll called “Quantum physics at face value”. It is exactly what the experimental evidence tells us: that particles exist in a superposition of all their possible states (eigenstates) in parallel - up until an interaction with a system that is ultimately entangled with an observer, a process we call decoherence, and then those alternative possibilities seemingly “disappear”, or - as other interpretations call it - collapse.

But where do they go? This is the central mystery of quantum physics. Yet, the onus is really on the other interpretations of experimental results to explain this. This is why Sean Carroll says that any competing theory of quantum mechanics should really be called “Disappearing Worlds” theories, simply because they must in fact explain what happens to these other apparent worlds. The only theory that actually makes sense is Many Worlds. Except for the problem of probability.

That is, the probability of why we experience one particular state, and not the (often) infinite other states. Why is this mundane world the one we experience and not the multitude of bizarre other worlds that seem to be possible?

The probabilities associated with different states is dictated by the Born rule. The Schrödinger equation gives us the “wave function” of possible states, and the Born rule simply says “take ones of those values, square its amplitude, and there you have the probability of experiencing it”. Why, though? Why specifically a quadratic fall-off in probability, the further out the values go?

With CACHI we have a plausible explanation, and it has an AIT foundation: when looking at generative programs under CHI constraints (that is, where the length of the program (Approximate Kolmogorov, K) and steps taken to execute it (T, Computational Depth) are kept constant, under minimal program change), deviations from higher-level patterns have a tractable penalty that is quadratic in nature. This is because complexity is measured in two dimensions: program length (an approximation of Kolmogorov complexity) and execution steps (computational depth). Multiplied together we have the complexity cost.

In a classical world, everything that happens is governed by patterns - by abstractions that are re-used. To re-use an existing pattern has minimal cost. Let’s look at a simple Cachi-Forth example to demonstrate this.

Take a look at this simple Cachi-Forth program:

10 5 + out

If you’re unfamiliar with the Cachi-Forth language, I’ll explain what it means. Cachi-Forth is a stack-based language that is run from left to right, one instruction at a time. An instruction is either a number, that tells is to put that number on a virtual, invisible “stack” (think a stack of cards). Or the instruction can be an operator like +, which tells it to take the top two values off that stack, add them together, and then put a new card on the stack with the result.

In this case, this program puts 10 on the stack, then 5, then runs addition (+) - which pops two values off the stack, adds them, and puts the result back on. Finally it runs “out” which pops a value off the stack and outputs it, which in this case would be the sum of 10 and 5: 15.

The complexity cost of this program is 4 (the number of instructions) multiplied by 4 (the number of execution steps), which is 16.

The two numbers can differ, though. If we use the conditional instruction: PRUNE, which terminates the program if the value on the stack is less than 64. Like this:

10 5 + out prune 20 out

In this case the PRUNE instruction will have 15 on the stack, which is less than 64, and so it will terminate and not run the final two instructions (which output 20). That means the length of the program is now 7, but the computational depth (execution steps) is 5. That makes the total complexity cost 7x5=35.

The computational depth can get wildly different to the length when you have loops and function calling. This is why it’s so important to understand just how much work is being undertaken in a program - the length alone isn’t enough.

Now let’s move on to something more relevant. Here is a pattern that very superficially models the motion of a particle through a one dimensional lattice:

>propagateX loop 10 + dup out end end

In this example, the first part “>propagateX” is a function declaration. The bit between there and the final “end” is the function body: the instructions that make up that function.

The body of the function is this “loop 10 + dup out end”. That, as you may have guessed, is a loop instruction. It pops a value off the stack and repeats the loop body (the between between “loop” and “end”) that many times. The loop body is “10 + dup out” - which pushes 10 on the stack, adds the two numbers on the stack together, duplicates them (so there’s now two of those values on the stack), and then pops one and outputs it (“out”).

This is a function, but in CACHI terminology we call it an abstraction. This is because it can be invoked without knowing the internals of its function body, with the understanding that it will do something in particular. We only care about the outcome. This is important in CACHI because these abstractions work to absorb sensory input data - that is, to accept input data - critical to seed the minimal change required in the generative program of the mind - without that input data perturbing the complexity cost outside of its homeostatic threshold. To do this it must anticipate the input to some degree.

So if this generative program was confronted with the values of a particle’s motion, say progressively along this one dimensional lattice as 10 20 30 40 50 60 70 80 90 100 - we could absorb this by invoking the function with, say, the parameters 0 and 10 (to count up, from zero, in tens 10 times):

>propagateX loop 10 + dup out end end
0 10 @propagateXY

You can run this yourself here.

For simplicity we’re going to presume that whatever it outputs is what it would expect the sensory data to provide (for technical completeness, we could use if-conditionals to match input data with that).

So for that program above, what exactly is the complexity cost? Our formula lets us calculate it quite easily, which luckily the Cachi-Forth interpreter does for us in its metrics: The length is 11, the steps of execution is 44, which makes the total cost 484.

Now let’s say this complexity cost is what we need to maintain in order to maintain consciousness. It cannot go lower and it cannot go higher. Yet the program must minimally-change each moment.

That even means that a program such as:

0 12 @propagateX

…which has the same length but would produce a similar list but up to 120 instead, taking extra steps and thus producing a complexity cost of 572. If this is outside of our threshold, then this program would be invalid. And this would dictate that our sensory input must be limited - ie. we can only look at one portion at a time (which maybe explains why we have moving eyeballs with a narrow field of vision).

So that deviation would cost 572 - 484 = 88 more steps. But perhaps that’s tolerable within our threshold band. We must assume that there is some tolerance band involved here (and it may even be computable what that is for the human brain).

For the purposes of this article, we’re going to assume there is indeed a tolerance band and that in this case it is 100. That means we can allow the program to mutate such that the cost is no greater or less than 100 - somewhere between 384 and 584.

This means that the program variation above would in fact be available to us consciously. In fact, there are many variations that would be available if we were to maintain that band. It would anticipate all of them successfully.

That means even code like this would be valid:

0 20 @propagateX

But it must still follow the same pattern of going up in 10s. Now what about anomalous output, like it counting up to 100 and then outputting 101? We can’t use the propagateXY function for that, so it would have to be an additional instruction or two:

0 10 @propagateX 101 out

The cost of that program is 598 - just outside our threshold.

What does this tell us? That anomalies are harder to be conscious of. It’s much easier for patterned extensions to be absorbed.

But what’s particularly interesting here is the cost of greater deviations in patterns. If we wanted to extend that anomaly further, outputting 101 and then 107, it would also need additional instructions:

0 10 @propagateX 101 out 107 out

The cost of this is 720.

If we were to look at the anomaly-generating instructions alone, we’ll see that the cost of “101 out” is 4 (2 instructions * 2 steps), and “101 out 107 out” is 16 (4 instructions, 4 steps). This shows a quadratic scaling factor: as the deviation rises, the complexity cost rises quadratically, because of these two orthogonal measures: program length and execution steps.

In terms of what we can then be conscious of, this shows a quadratic penalty on our ability to be conscious of anomalies. How would this be experienced? Statistically, it would be experienced as a probability. And this is broadly why we say that CACHI can form the basis of a Born-rule derivation in quantum physics.

As soon as that number becomes an intrinsic part of a much greater pattern, then the cost of deviating from that pattern even slightly becomes far too large to absorb: the consequential impact on processing would alter the computational depth drastically.

This, then, reflects the point of “decoherence”, entanglement with a classical environment consisting of large abstractions. It’s only at the freer, minuscule, inconsequential level of individual particles prior to involvement, that we get a glimpse of these alternative program mutations that are closely within the tolerance bands - because only at the level of the inconsequential can the variations in the generative program still fall within that complexity tolerance band.

What would be an example of a consequential interaction? Well, being picked up by a measuring device is a classic example. The measuring device can only measure one result, for it to be capable of doing otherwise would require effectively multiple measuring devices to exist - each processing separate results. For us to be conscious of all the mechanics leading up to those multiple devices existing in parallel would simply be far outside of our complexity homeostasis, and so it’s impossible for us to be conscious of it - and this is what we mistakenly call the collapse of the wave function.

Let’s look at a Cachi-Forth example. We’ll replicate the same idea of a particle motion on a one-dimensional lattice, but this time the output will feed into another function called “measure”, that will take the output that came before it and make it part of a more elaborate process - in our case a cumulative loop.

>propagateX loop 10 + dup end end
10 10 @propagateX bval + + + loop bit end bval out

The complexity cost of this is about 1,995. But if we perturb the start of the program, changing the 10 to a 120, the complexity rises to 7,733 - a 5,738 cost difference. Compare that to the previous perturbation that cost a C of just 4. That’s because those values at the front are entangled with the larger abstractions - in this case the loop in the main part of the program. That entanglement is effectively what constitutes a kind of decoherence, because any small change to it pushes the complexity cost way out of bounds. This excludes any variations at that small level.

That entanglement gives that single value inertia - a resistance to change. You can see the calculated inertia by selecting that 120 and clicking “Calc Inertia” - using a Monte Carlo simulation it will derive an expected cost delta of the overall percentage from changing that number. Entangled instructions will be much higher - in this case about a 63% drop in overall cost - well outside of what would be expected with CHI constraints.

And this is what entanglement and decoherence basically are: inertia. Entanglement is relative inertia (relative to another part of the program), and decoherence is inertia relative to the observer - the final outcome.

So this shows us - when CHI is applied in the Many Worlds of Everettian Quantum Mechanics, there is no collapse. There is merely an infinitude of non-experiencable outcomes, that become non-experiencable as soon as its values are needed to support a particular outcome.

This is the first part of a multi-part series of articles where we will be going into the ramifications of an AIT, complexity-homeostatic understanding of quantum mechanics. In the next part we’ll look at the math of the derivation more closely.